PHYSIK → Klasse 11 & 12 → Harmonische Schwingungen

Einstieg

1. Bewegungen Synchronisieren
   Material: 1x Federpendel, 1x Stufenlos regelbarer Motor (ca. 120 U/min), 1x Lampe
   
   Vorbereitung: Pendel und Motor sollen so aufgestellt werden, dass sich die Schatten beider Objekte überlagern.
   
   Link zum Video
   
   Durchführung: Synchronisiere die Schatten von Pendel und Motor.
   
   Auswertung:
   1. Interpretiere die Überlagerung beider Bewegungen.
      Hinweis: Kooridnaten entlang eines Kreises können mithilfe von \(\sin x\) und \(\cos x\) beschrieben werden.
2. Die folgende Abbildung zeigt, wie eine Schwingung durch eine Kreisbewegung beschrieben werden kann.
   
   1. Beschreibe die Abbildung.
   2. Stelle einen Ausdruck für die Auslenkung des Pendels \(y(t)\) für beliebige Winkel \(\phi(t)\) auf.
   3. Bei der Kreisbewegung des Motors erhöht sich der Winkel der Kreisbewegung linear mit der Zeit. Die sogenannte Winkelgeschwindigkeit \(\omega\) ist also konstant. Um wie viel erhöht sich der Winkel pro Sekunde, wenn die Periodendauer des Pendels 2s beträgt? Drücke das Ergebnis als Vielfache von \(\pi\) aus.

   Lösung:

   Zu 2.:
   Die Auslenkung des Pendels wird durch eine Sinusfunktion beschrieben, welche um die maximalke Auslenkung \(\hat{y}\) gestreckt wurde: \[y(t)=\hat{y}\sin(\phi(t))\] Zu 3.:
   Die Rotationsgeschwindigkeit des Motors soll konstant sein. Wenn dieser innerhalb von 2 s einen Winkel von 360° (\(2\pi\)) überstreicht, so gilt für die Winkelgeschwindigkeit: \[\omega=\frac{360°}{2s}=\frac{2\pi}{2s}=\pi\frac{1}{\rm{s}}\] Für den Winkel der Kreisbewegung gilt damit \[\phi(t)=\omega t=\pi\frac{1}{\rm{s}}t.\]

Aufgaben

1. Im Folgenden wollen wir den bisher nur experimentell bestimmten Ausdruck für die Periodendauer eines Federpendels \[T=2\pi\sqrt{\frac{m}{D}}\] mithilfe des linearen Kraftgesetzes theoretisch herleiten.
   etwas mehr als \(2\pi\).
   1. Für das Federpendel lautet das lineare Kraftgesetz: \[F(t)=-D\cdot y(t)\] Warum spielt die Gravitationskraft hier keine Rolle mehr?
   2. Erläutere die Bedeutung des negativen Vorzeichens in der Gleichung.
   3. Für das Pendel gilt die Newtonsche Bewegungsgleichung \[F(t)=m\cdot a(t),\] sodass die Bewegung des Pendels durch folgende Differentialgleichung beschrieben wird: \[-D\cdot y(t)=m\cdot a(t)\] oder \[-D\cdot y(t)=m\cdot \ddot{y}(t)\] Setze unseren Ansatz \[y(t)=\hat{y}\sin(\omega t)\] in die Differentialgleichung ein und bestimme \(\omega\) so, dass die Gleichung für beliebige \(m\) und \(D\) zu allen Zeiten \(t\) erfüllt ist.
   4. Leite mit dem gewonnenen Ausdruck für \(\omega\) den gesuchten Ausdruck für die Periodendauer her.

   Anmerkung: Wir haben herausgefunden, dass \[T\approx 2.02 \sqrt{\frac{m}{N}} \sqrt{m}\] In dem Zahlenwert \(2.02\) steckt nun noch \(\frac{1}{\sqrt{D}}\), wobei \(D=14 \frac{\rm{N}}{\rm{m}}\) war. Entsprechend können wir den Ausdruck etwas umschreiben: \[T\approx 2.02 \sqrt{\frac{m}{N}} \sqrt{m}=2.02 \cdot \sqrt{14 \frac{\rm{N}}{\rm{m}}}\sqrt{\frac{m}{14 \frac{\rm{N}}{\rm{m}}}}\] \[\approx 7.6 \sqrt{\frac{m}{14 \frac{\rm{N}}{\rm{m}}}}\] Wir erhalten also als Vorfaktor \(7.6\), welcher zumindest in der Größenordnung von \(2\pi\) ist.

   Herleitung des linearen Kraftgesetzes beim Federpendel:

   Achtung: \(x(t)=y(t)\)
   1.1 Setting
   Auf die Masse wirkt einerseits die Gravitationskraft \[F_G=-m\cdot g,\] welche mit einem negativen Vorzeichen versehen werden muss, da die Kraft nach unten zeigt und somit auch eine negative Beschleunigung (also entgegengesetzt zu \(x(t)\)) als Folge haben muss.
   
   
   Andererseits wirkt die Spannkraft der Feder \[F_S(t)=-D\cdot s(t)\] wobei \(s(t)\) die momentante Auslenkung aus ihrer Anfangsauslenkung ohne Masse ist. Auch die Spannkraft muss mit einem negativen Vorzeichen versehen werden, da sie für negative Auslenkung \(s(t)\) nach oben gerichtet und für positive Auslenkungen nach unten gerichtet sein muss.

   

   

   

   1.2 Resultierende Kraft
   Sei \(x_0\) der Abstand der Anfangslage zur Gleichgewichtslage, so gilt: \[s(t)=x(t)-x_0.\] Damit lässt sich die resultierende Kraft auf die Masse rekonstruieren: \[F_{res}(t)=F_G+F_S(t)=-m\cdot g -D\cdot (x(t)-x_0)\] Da sich in der Gleichgewichtslage \(x(t)=0\) Gravitationskraft und Spannkraft gegenseitig kompensieren folgt: \[F_{res}=-m\cdot g +D\cdot x_0=0\] \[\Leftrightarrow\quad -m\cdot g= -D\cdot x_0.\] 1.3 Lineares Kraftgesetz
   Die Gravatiationskraft ist also durch die Gleichgewichtslage fest bestimmt, sodass wir diese im Ausdruck oben ersetzen können: \[ \begin{eqnarray} F_{res}(t)&=& -m\cdot g -D\cdot (x(t)-x_0)\\ &=& -D\cdot x_0 -D\cdot (x(t)-x_0)\\ &=& -D\cdot x(t). \end{eqnarray} \] Wir sehen also, dass in der resultierenden Kraft die Gravitationskraft durch die Verschiebung in die Gleichgewichtslage eliminiert wird.
   
   1.4 Aufstellen der Bewegungsgleichung
   Mit der Newtonschen Bewegungsgleichung für die Masse \(m\) \[F_{res}(t)=m\cdot \ddot x(t)\] folgt: \[m\cdot \ddot x(t)=-D\cdot x(t)\] bzw. \[\ddot x(t)=-\frac{D}{m}x(t).\]

2. 1. Bestimme die Periodendauer eines Federpendels mit einer Masse von 6 kg und einer Federkonstante von 40 N/m.
   2. Bestimme die Masse eines Federpendels, wenn die Federkonstante 14 N/m und die Periodendauer 1.1 s beträgt.
   3. Bestimme die Federkonstante eines Federpendels, wenn die Masse 400 g und die Periodendauer 4 s beträgt.
3. Ein Federpendel führt eine harmonische Schwingung aus. Zum Zeitpunkt \(t=0\rm{{s}}\) befindet sich das Pendel in der Phase \(\phi(0)=0\) (Ruhelage). Die maximale Auslenkung (Amplitude) des Pendels beträgt 10 cm und die Winkelgeschwindigkeit \(\frac{\pi}{2\rm{s}} \).
   1. Stelle die Funktion der Auslenkung \(y(t)\) auf und plotte diese.
   2. Bestimme die Phase des Pendels nach 1 s, 2 s und 5 s. Gib die Phase auch in 1° an.
   3. Bestimme die Periodendauer der Schwingung.
   4. Bestimme die Auslenkung des Pendels nach 1 s, 2.3 s und 4.2 s.
   5. Plotte die Geschwindigkeitsfunktion \(v(t)\) und die Beschleunigungsfunktion \(a(t)\) der Schwingung.
   6. Bestimme die Geschwindigkeit und die Beschleunigung des Pendels an den Umkehrpunkten, in der Ruhelage und nach 4.2 s.

   Lösung:

   

4. 1. Zum Zeitpunkt 4 s hatte ein Pendel mit der Winkelgeschwindigkeit \(\frac{\pi}{2\rm{s}} \) und der Amplitude 10 cm eine Auslenkung von 10 cm. In welcher Phase muss das Pendel dann zum Zeitpunkt \(t=0\rm{s}\) gewesen sein?
      Hinweis: Die Phase bezieht sich immer auf die Auslenkung des Pendels, d.h. welcher Winkel muss beginnend von 0° verstrichen worden sein, damit das Pendel die vorgegebene Auslenkung besitzt.
   2. Stelle einen Ausdruck für die Auslenkung \(y(t)\) auf, wenn das Federpendel allgemein nicht in der Phase \(\phi(0)=0\) startet, sondern in der Phase \(\phi_0\). Plotte anschließend die entsprechende Funktion mit frei wählbaren Parametern \(\omega\), \(\hat{y}\) und Startphasenwinkel \(\phi_0\).

   Lösung:

   

5. Fadenpendel
   

   
   Für das Fadenpendel bei kleinen Auslenkungen von maximal 10° lautet das lineare Kraftgesetz \[F(t)=-\frac{mg}{l}y(t),\] mit der Fadenlänge \(l\), der Masse des Pendelkörpers \(m\) und dem Ortsfaktor \(g\).
   1. Warum tritt der Ortsfaktor in dem linearen Kraftgesetz auf?
   2. Leite den Ausdruck für die Periodendauer des Fadenpendels her: \[T=2\pi\sqrt{\frac{l}{g}}\]
   3. Plane ein Experiment, in dem du die hergeleitete Formel überprüfst. Fertige ein vollwertiges Versuchsprotokoll samt geeigneter Auswertung an. Welche Komponente in der Formel lässt sich nicht weiter untersuchen? Tipp: Hänge das Pendel bifilar auf.

   Herleitung des linearen Kraftgesetzes beim Fadenpendel:

   

   Auf das Fadenpendel wirkt ausschließlich die Gravitationskraft. Für die Pendelbewegung ist jedoch nur der Anteil der Gravitationskraft entlang der Bewegungskurve relevant, der restliche Anteil wird durch den Faden kompensiert. Der Anteil entlang der Bahnkurve ist entsprechend der Abbildung \[\textcolor{red}{F(t)}=-\textcolor{darkgreen}{F_g}\sin(\textcolor{brown}{\alpha(t)}),\] wobei \(\textcolor{brown}{\alpha(t)}\) der momentane Auslenkungswinkel des Pendels ist, nicht zu verwechseln mit dem Phasenwinkel \(\phi(t)\) der assoziierten Kreisbewegung.
   Weiterhin gilt für die vom Pendel zurückgelegte Kreisbogensträcke von der Ruhelage \[\textcolor{darkblue}{y(t)}=l\textcolor{brown}{\alpha(t)}.\] Durch Quotientenbildung erhält man \[\begin{eqnarray} \frac{\textcolor{red}{F(t)}}{\textcolor{darkblue}{y(t)}}&=&\frac{-\textcolor{darkgreen}{F_g}\sin(\textcolor{brown}{\alpha(t)})}{l\textcolor{brown}{\alpha(t)}}\\ \Leftrightarrow \textcolor{red}{F(t)}&=&-\frac{\textcolor{darkgreen}{F_g}}{l}\frac{\sin(\textcolor{brown}{\alpha(t)})}{\textcolor{brown}{\alpha(t)}}\textcolor{darkblue}{y(t)} \end{eqnarray}\] Für kleine Winkel lässt sich die Sinusfunktion nähern (Taylorentwicklung): \[\sin(\textcolor{brown}{\alpha(t)})\approx\textcolor{brown}{\alpha(t)}\] Damit folgt: \[\textcolor{red}{F(t)}=-\frac{\textcolor{darkgreen}{F_g}}{l}\frac{\textcolor{brown}{\alpha(t)}}{\textcolor{brown}{\alpha(t)}}\textcolor{darkblue}{y(t)}=-\frac{F_g}{l}\textcolor{darkblue}{y(t)}\] Und mit \(\textcolor{darkgreen}{F_g}=mg\) folgt: \[\textcolor{red}{F(t)}=-\frac{\textcolor{darkgreen}{F_g}}{l}\frac{\textcolor{brown}{\alpha(t)}}{\textcolor{brown}{\alpha(t)}}\textcolor{darkblue}{y(t)}=-\frac{mg}{l}\textcolor{darkblue}{y(t)}\]

6. Induktionsstrom und Schwingungen
   Material: 1x Spule ca. 1200 Windungen, 1x Oszilloskop, 1x Feder, 1x Gewichtsteller, 1x Magnet, 1x Stativ, Kabel
   
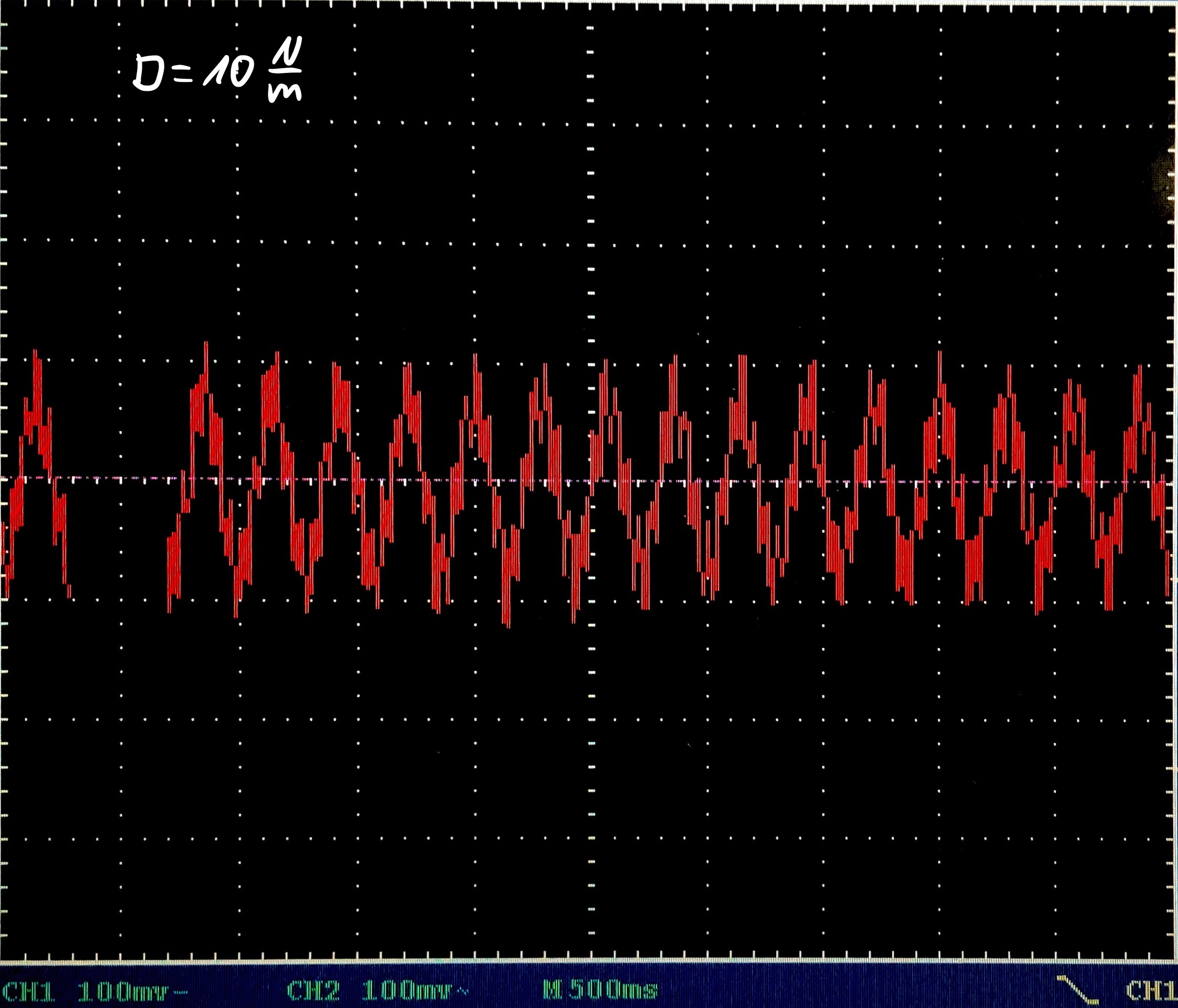
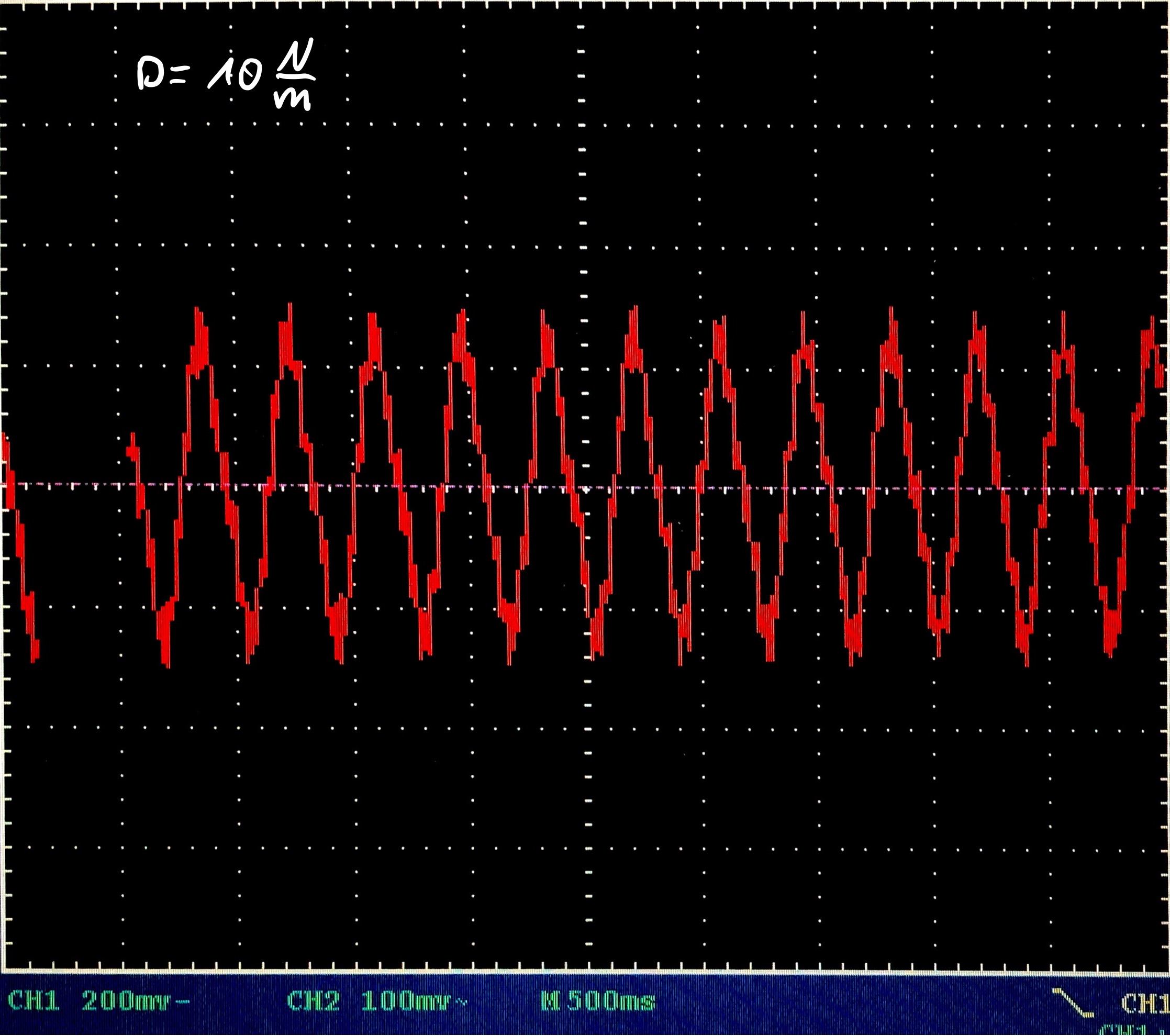
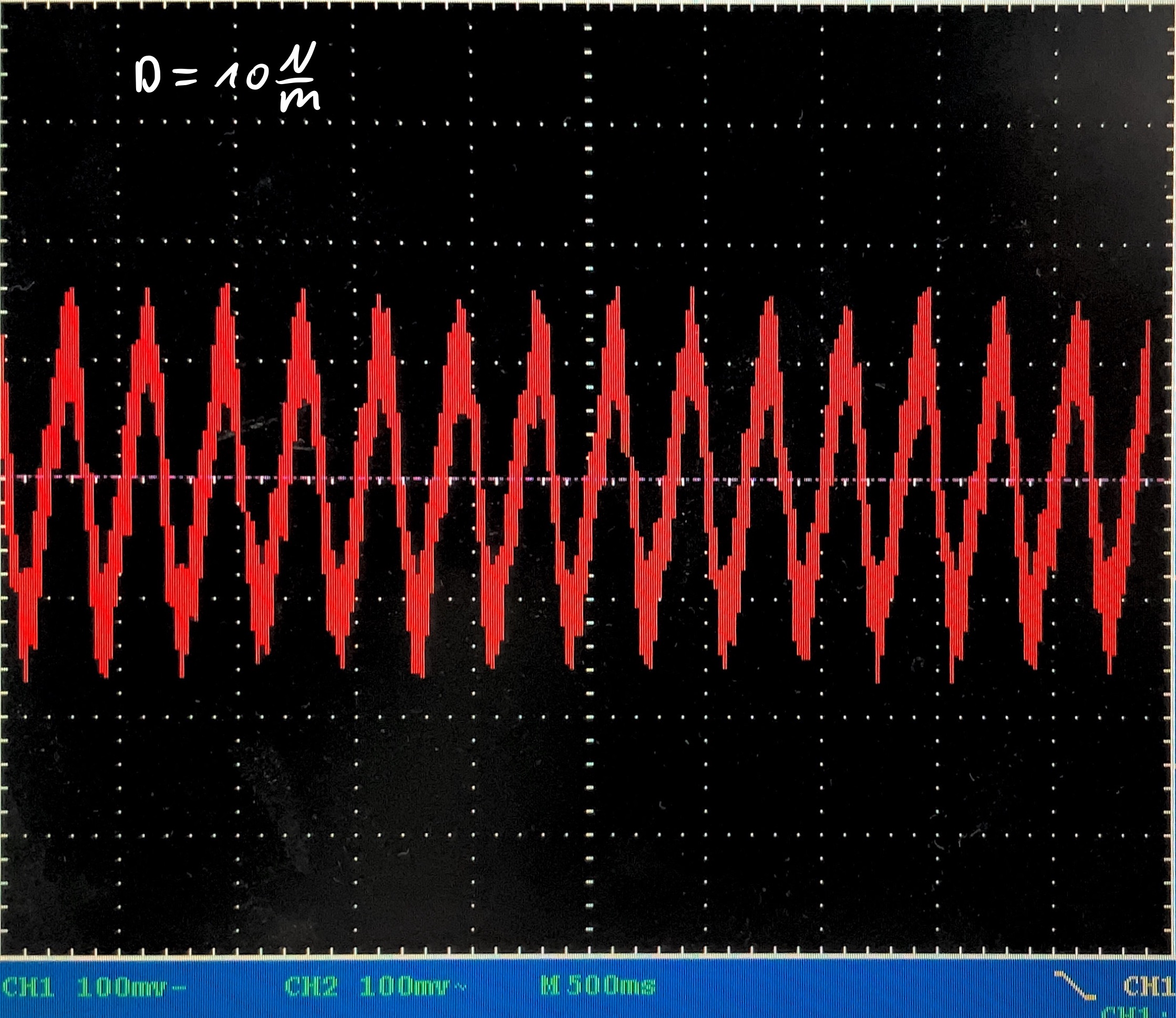
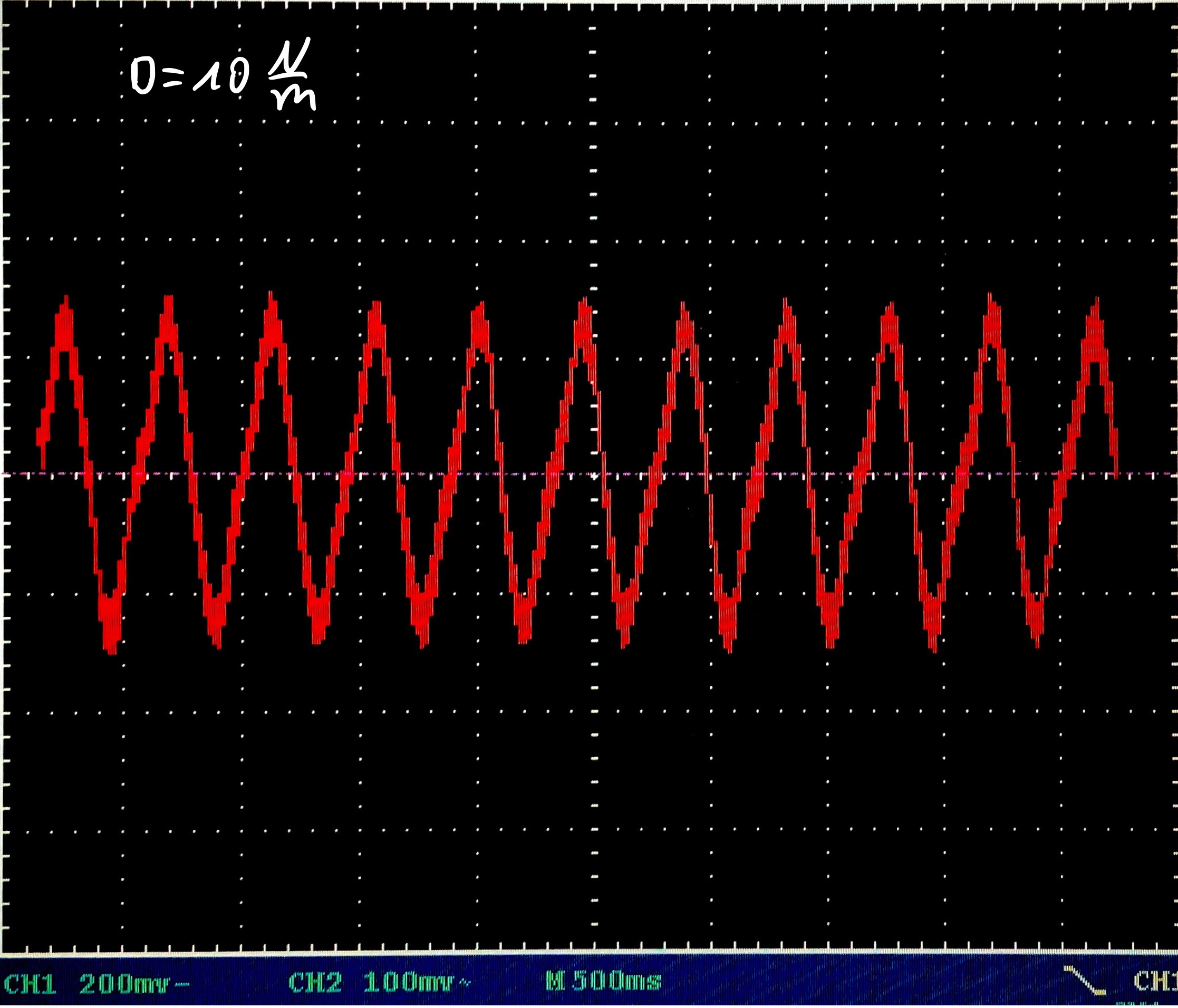
   Vorbereitung: Befestige den Magnet an dem Gewichtssteller und hänge den Teller an der Feder und anschließend an dem Stativ auf. Positioniere den Magneten so, dass er in ca. 1/4 der Spule herrein ragt. Schließe die Spule an das Oszilloskop an. Stelle das Oszilloskop auf einen geeigneten Messbereich ein (\(V_{max}=400\rm{mV}\), \(t_{max}=5\rm{s}\))
   
   
   
   Durchführung: Lasse die Feder leicht schwingen. Speichere die Spannungswerte auf dem Oszilloskop. Wiederhole den Vorgang für verschiedene Massen auf dem Gewichtsteller.
   
   Auswertung:
   1. Erkläre das Entstehen der Spannungskurve auf dem Oszilloskop.
   2. Bestimme die Periodendauer der verschiedenen Schwingungen und damit die Masse für jede Messung.
   3. In einer weiteren Versuchsreihe wurden folgende Werte für die Periodendauer in Abhängigkeit von der Federkonstante bei konstanter Masse aufgenommen: \[ \begin{array}{|c|c|} \hline \text{Federkonstante in N/cm}&\text{Periodendauer in s} \\ \hline 0.035 & 7.5 \\ \hline 0.055& 5.9 \\ \hline 0.075 & 5.1 \\ \hline 0.095 & 4.6 \\ \hline 0.115 & 4.1 \\ \hline 0.135 & 3.8 \\ \hline \end{array} \] Zeige mithilfe der Messreihe, dass \(T\sim D^{-\frac{1}{2}}\) gilt. Bestimme mithilfe der Proportionailtätskonstante die Masse des Pendels.

   Messwerte am Oszilloskop:

   

   

   Arbeitsblatt zum Ausdrucken der Messwerte