MATHE → Klasse 7 & 8 → Lineare Funktionen

Einstieg

1. In der 8a und 8b befinden sich 26 Schüler:innen. Pro Schuljahr verlassen in der 8b im Schnitt 1.25 Schüler:innen die Klasse, weil sie nicht für Mathe richtig gelernt haben. In der 8a sind es sogar 2 Schüler:innen pro Jahr.
   1. Stelle die Funktionsgleichung für beide Zusammenhänge auf.
   2. Zeichne die Funktionsgraphen.
   3. Was beeinflusst in der Funktionsgleichung, wie Steil der Graph fällt?
2. 
   Die Achterbahn Colossos im Heide Park hat eine maximale Neigung von 61°. Dies entspricht einem Gefälle von 180%, also auf 100 m horizontaler Strecke werden 180 m Höhe abgenommen. Die steilste Abfahrt beginnt jedoch schon ab einer Höhe von 60m.
   
   1. Stelle die Funktionsgleichung für den Funktionsgraphen auf.
   2. Wo lässt sich in der Funktionsgleichung die Neigung wiederfinden?
3. Welche Informationen benötigt man, um Funktionen wie in Einstiegsaufgabe 1 und 2 vollständig zu beschreiben?

Aufgaben

1. Methoden
   Die Durschnittstemperatur in Sibirien beträgt ca. 1°C. Durch den Klimawandel nimmt die Durschnittstemperatur jedoch um \(\frac{1}{10}\)°C pro Jahr zu.
   1. Stelle die Funktiosngleichung auf.
   2. Finde eine Methode, mit der sich der Funktionsgraph (Gerade) möglichst schnell zeichnen lässt.

   Lösung:

   1. Die Funktionsgleichung lautet: \[f(x)=\frac{1}{10}x+1\]
   2. Zum Zeichnen des Funktionsgraphen gibt es zwei Möglichkeiten neben dem Anfertigen einer Wertetabelle:
      
      1. Steigungsdreieck:
         Hierbei wird zunächst der \(y\)-Achsenabschnitt \(b\) im Koordinatensystem markiert. Anschließend wird von diesem Punkt mithilfe eines Steigungsdreiecks die Steigung der Funktion eingezeichnet. Das Steigungsdreieck hat eine geschickt gewählte Breite \(\Delta x\), die Höhe ist dann \[\Delta y =m \cdot \Delta x.\]
         
      2. Zwei Punkte:
         Hierbei berechnet man mithilfe der Funktionsgleichung zwei Punkte \(P_1\) und \(P_2\) auf dem Funktionsgraphen. Die Gerade des Funktionsgraphen ist durch zwei beliebige Punkte eindeutig festgelegt.
         

2. Beschreibe das Vorgehen zum Zeichnen der beiden Funktionsgraphen.
   
   
   
   
   
3. Zeichne die Funktionsgraphen folgender Funktionen:
   1. \(f(x)=3x-1\)
   2. \(f(x)=x+1\)
   3. \(f(x)=-0.5x-1\)
4. Mithilfe von GeoGebra können die Funktionsgraphen von Funktionen schnell dargestellt werden.
   
   1. Beschreibe den Einfluss der Parameter \(m\) und \(b\) auf den Funktionsgraphen einer linearen Funktion.
   2. Plotte selber die Funktion \(g(x)=-0.3x+2\).
5. Gegeben sei folgender Funktionsgraph.
   
   1. Bestimme mithilfe des Steigungsdreiecks die Steigung und damit die Funktionsgleichung.
   In diesem Video wird nochmal die Methode mit dem Steigungsdreieck erklärt.
6. Lineare Funktionen in der Schule
   Finde in der Schule zwei verschiedene Orte, an denen eine Schräge durch eine lineare Funktion beschrieben werden kann.
   1. Mache ein Foto von dem Ort.
   2. Bestimme mithilfe eines Zollstocks die Steigung und den \(y\)-Achsenabschnitt der linearen Funktion.
   3. Stelle die Funktionsgleichung auf und zeichne den Funktionsgraphen.
   Idealerweise hat eine der Funktionen eine negative Steigung.
7. Kleine Denkaufgabe
   Um die Straße am Fuße des Berges mit der Straße auf dem Berg zu verbinden, ist es sinnvoll die Verbindungsstraße als Serpentinenstraße anzulegen. Angenommen der Straßenverlauf kann durch lineare Funktionen beschrieben werden, deren Steigung nicht 0.08 übersteigen darf. Desweiteren können die Serpentinen nicht breiter als 100m lang sein.
   
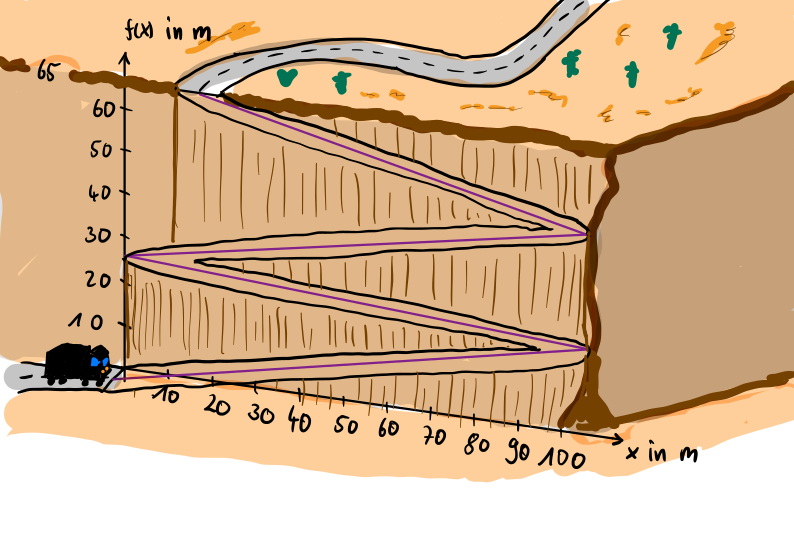
   1. Berechne die minimale Anzahl an benötigten Serpentinen.